关于机器学习的一些总结

以下是自己在机器学习课程中的一些知识点总结，主要渗透了自己对某些知识点的理解，涵盖的面较广，将会不定期地更新。若有理解不一致之处，望指明并相互探讨。

1 SVM中常用的核函数有哪些？如何选择相应的核函数？

常用的核函数有线性核，多项式核以及高斯核。

1.1 线性核

$\kappa (x,z) = < x,z >$ κ ( x , z ) = x , z >

线性核对应的映射函数为：

$\phi (x) = x$ ϕ ( x ) = x

。即映射空间与原始空间是相同的。它适用于原始数据集是线性可分的情况。此时所使用的是线性SVM。

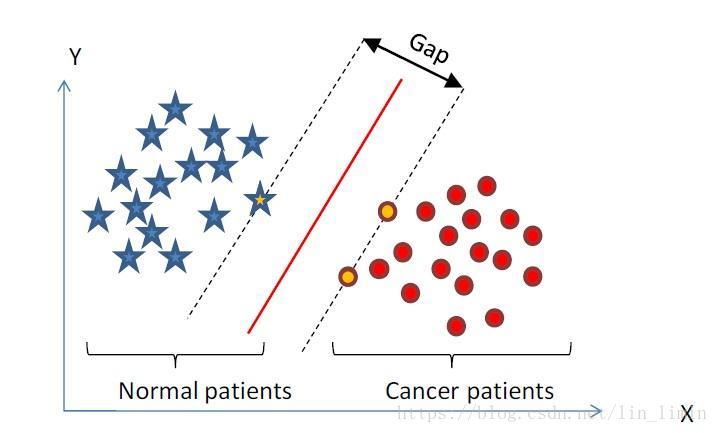
1.2 多项式核

$\kappa (x,z) = {[a &lt; x,z &gt; + c]^b}$ κ ( x , z ) = [ a < x , z > + c ] b

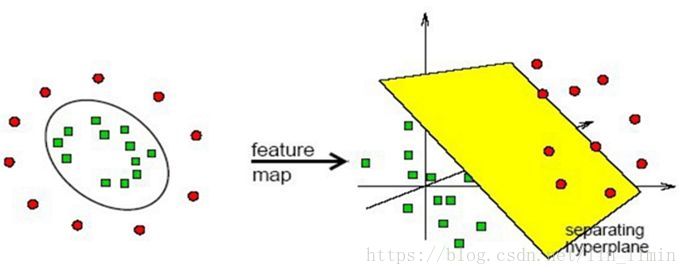
多项式核将数据从原始空间映射到了高维空间。

考虑数据集在原始空间的分布情况：如果分隔的决策面非线性且较为规则的话（比如，决策面是椭圆，椭球，双曲线等），可以考虑使用多项式核。

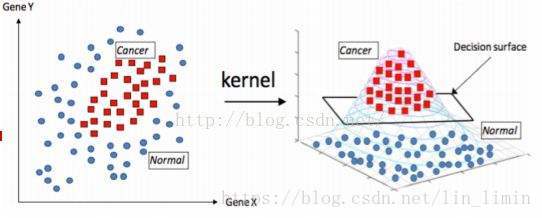
1.3 高斯核

$\kappa (x,z) = \exp ( - \frac{{{{\left\| {x - z} \right\|}^2}}}{{2{\sigma ^2}}})$ κ ( x , z ) = exp ( − 2 σ 2 ∥ x − z ∥ 2 ​ )

高斯核将数据从原始空间映射到了无限维空间。关于高斯核与多项式核的关系，可以参见这篇文章： 关于支持向量机(SVM)的高斯核和惩罚因子C的理解（简单易懂） 。

当原始空间的决策面较不规则，难以使用多项式核进行分类的时候，可以考虑高斯核。因为多项式核只是将原始空间映射成高维空间，而高斯核将原始空间映射成了无限维，所以对应的决策面可以更复杂，可以使得数据更容易被划分（当然这样也就可能出现过拟合的情况，关于高斯核参数 $\sigma$ σ 的理解，上文 关于支持向量机(SVM)的高斯核和惩罚因子C的理解（简单易懂） 亦有介绍）。